课前任务

1. 了解大数定律产生的背景以及发展阶段

大数定律背景：在实际应用中，当试验次数很大时，便可以用事件的频率来代替事件的概率。更重要的是，这提供了一种思想，经验观测可以反映随机规律的这样一种思想。

大数定律的一般提法：当随机变量序列满足一定条件时，随机变量序列的算术平均值向各随机变量期望的算数平均值收敛的定律。

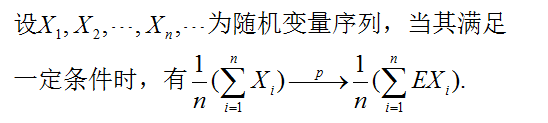
诞生阶段--伯努利大数定律，其在随机变量满足独立同分布且均服从二项分布条件下使用。

推广阶段--切比雪夫大数定理，其在随机变量满足独立（同分布、不同分布）且期望和方差有限，方差有共同上界的条件下使用。

发展阶段--辛钦大数定律，其在随机变量满足独立同分布且具有相同期望条件下使用。

2.关于大数定律的课前自测题

报纸上说，你所在城市的一家医院，这周出生的孩子中90%都是男孩，这真是一家有魔力的医院。根据你的概率知识，这种现象最有可能出现在什么样的医院呢？（）

A. 一定是城市里最大、最著名、最拥挤的妇幼医院。

B. 大概率是一家很小的私立医院或者社区医院。

C.大医院和小医院出现这种情况的概率是相等的，无法分辨医院的情况。

3.了解中心极限定理的相关背景

中心极限定理是指：随机变量序列部分和分布渐近于正态分布的一类定理。这类定理是数理统计学和误差分析的理论基础，其指出了大量随机变量之和近似服从正态分布的条件。

   “中心极限定理”之称谓颇为使人迷惑 ，哪里的“中心”？哪里的极限？真是令初学者一头雾水。中心极限定理的名称中，“中心”（Central）一词是指：随机变量的数量趋近于无穷大时，“随机变量的算术均值”趋近于正态分布的中心位置，即正态分布的期望。而“极限”（Limit）一词则强调了随机变量的数量近于无穷大时，随机变量的算术均值的分布趋近于正态分布的这种极限情况。

中心极限定理的历史背景：

1716年，棣莫弗对n重贝努利实验中每次实验事件A出现的概率为1/2的情况如何进行计算二项分布进行了讨论（n很大时二项分布计算很困难），后来拉普拉斯对其结论进行了改进得到如下定理：

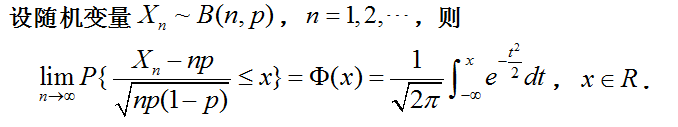
我们称之为二项分布的极限分布为正态分布的中心极限定理，即棣莫弗-拉普拉斯中心极限定理。该定理条件比较强，需要已知随机变量的分布（二项分布）。因此，列维-林德伯格将棣莫弗-拉普拉斯中心极限定理推广，只需要满足条件：随机变量序列独立、同分布、期望存在、方差存在即可。

中心极限定理的一般提法：

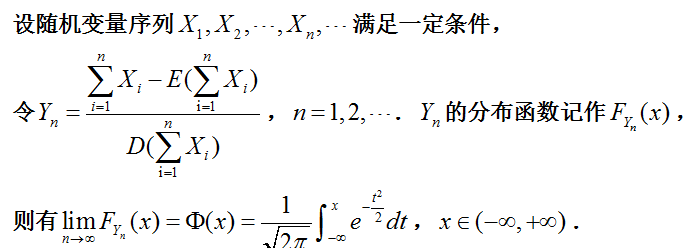
中心极限定理的意义：

中心极限定理不仅揭示了正态分布的存在性，还说明了正态分布普遍存在的原因——

在实际问题中，很多随机变量是由诸多独立同分布，且影响甚微的小因素叠加而成的，因此这些随机变量可近似刻画成服从正态分布的随机变量，这是正态分布普遍存在的原因，也是中心极限定理的客观背景。

4.中心极限定理的课前自测题

设某操作者在机床加工机械轴，使其直径符合规定要求，但加工后的机械轴与规定要求总有一定的误差，这是因为加工时受到一些随机因素的影响，比如，机床的加工状态、材料方面的影响、测量量具和技术方面的误差、车间环境影响、操作者注意力和情绪影响、以及其他许多可列出的影响因素，这些影响因素分别记为

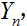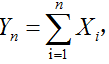则它们每个是很微小的、随机的且相互独立的，它们的综合影响使得每个加工轴的直径产生了误差，若将这个误差记为  则    .请选择下列正确的说法（ ），

（A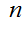） 很小时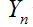， 近似服从标准正态分布。

（B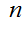） 很大时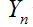， 标准化后近似服从标准正态分布。

（C）无论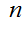 如何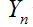， 近似服从指数分布。

课中

课后自学

1. 视频观看

2. 课后自测

1. 请用大数定律解释“久赌必输”的原因。

2.（保险中的相关问题）某保险公司准备推出一项新业务，经过决策层综合分析，该业务每份保单的年赔付金额 X 服从参数为0.001的指数分布，试建立每份保单的售价Q(单位元）与参保人数n的关系，使得保险公司在该项业务上有95%的把我处于盈利状态。