- 学校 合肥工业大学
- 学分 3
- 开课院系 汽车与交通工程学院
- 课时 48
- 专业大类 交通运输类
- 课程视频总时长（分钟） 0
- 开课专业 交通运输 交通工程
- 编号 1722022B
Course introduction课程简介
运筹学是一门研究资源运用及活动筹划的新兴学科，是交通运输类专业中一个最为重要的专业基础课之一。 本课程的目的在于了解和发现资源运用及活动筹划中的基本规律，提出科学的决策方法，以便更有效发挥有限资源的效益，从而达到总体有效或平衡的目标。通过本课程学习，学生可以掌握运筹学的思维方式，能应用系统的、科学的数学分析方法对系统进行定量化分析。通过建立数学模型和模拟模型，应用计算机技术求解，可以解决比较复杂的交通问题，达到资源优化配置、获得最优决策的目的。完成本课程的学习后，学生要掌握“四规划”和“两论”（线性规划、运输问题、整数规划、非线性规划、动态规划、图论和排队论）等的基本概念、基本理论和基本方法，熟悉运筹学模型在交通实践中的应用。
Teachers team教师团队
-
刘昊翔
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
目前主要从事交通运输管理领域的基础理论研究与应用，在城市交通网络设计建模、交通行为分析、交通规划管理与控制、电动汽车充换电设备选址、公共交通运营优化、数学优化算法等方面具有多年持续深入的研究与实践经验。先后发表期刊会议论文二十余篇，其中两篇入选ESI高被引论文。近年在城市交通网络设计领域等开展了持续而深入的研究工作，取得了一系列的研究成果，研究论文发表或录用在交通科学与技术领域顶级期刊《Transportation Research Part B》和国际知名期刊《Transportation Research Part E》、《Networks and Spatial Economics》及《Transportmetrica A》等上。
查看全部
-
于旸
合肥工业大学 ｜ 汽车与交通工程学院
研究方向：
查看全部
动态交通分配，交通系统建模、仿真、优化，复杂交通网络，交通规划，交通行为，交通大数据
发表论文：
Yu,Y., Han,K., Ochieng,W.O., 2020. Day-to-Day Dynamic Traffic Assignment with Imperfect Information, Bounded Rationality and Information Sharing.
Transportation Research Part C 114 (2020), 59-83.Yang Yu, Ke Han. Day-to-Day Dynamic Traffic Assignment with Imperfect Information and Information Sharing Behaviour. Transportation Research Board 99th Annual Meeting, Washington, D.C., Jan 2020.
教育经历：
西南交通大学 交通工程 2010.09 – 2014.06 学士
帝国理工学院 Transport 2014.10 – 2015.10 硕士
帝国理工学院 Transport 2016.06 – 2021.06 博士 .
-
龙建成
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 教授
龙建成，合肥工业大学教授、博士生导师。主要研究方向为城市交通网络优化与管理、城市动态交通分配理论与方法、共享交通系统建模与优化、公共交通运营与管理等。近年来，先后主持国家自然科学基金项目5项（包括青年基金、面上、优青、杰青）、教育部新世纪优秀人才支持项目、霍英东教育基金会高等学校青年教师基金项目、中国博士后科学基金项目、安徽省重大科技专项项目等；在国内外重要期刊上发表论文70余篇，包括在领域顶级期刊《Operations Research》上发表论文3篇（一作2篇）、《Transportation Science》上发表论文1篇（一作）、《Transportation Research Part B》上发表论文13篇（一作或通讯10篇）。其它论文主要发表在《Transportation Research Part C\D\E》、《IEEE Transactions on Intelligent Transportation Systems》、《European Journal of Operational Research》、《Networks and Spatial Economics》、《系统工程理论与实践》等期刊上。博士学位论文“城市道路交通拥堵传播规律及消散控制策略研究”获2012年全国优秀博士学位论文提名论文，2013年入选教育部新世纪优秀人才支持计划，动态交通分配方面的研究成果曾入选了国家自然科学基金委2014年年度报告，2015年获得国家自然科学基金优秀青年科学基金，2017年入选教育部“长江学者奖励计划”青年学者，2018年获教育部自然科学一等奖1项，1篇论文入选《中国科学》“2018年十年持续影响力论文奖”，2019年获得国家杰出青年科学基金，2021年获安徽省教科文卫体系统职业道德先进个人,2022年获安徽省教学成果二等奖1项。现任学术期刊《Digital Transportation and Safety》高级副主编、《控制与决策》和《交通运输系统工程与信息》等编委、管理科学与工程学会常务理事、安徽省非线性科学学会副理事长、管理科学与工程学会交通运输管理分会副主任等。
查看全部
-
丁建勋
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
合肥工业大学本科毕业（双专业：主修管理，辅修计算机）和博士后（管理科学与工程）出站，北京航空航天大学硕士和博士（交通运输规划与管理），东京大学西城教授课题组交流学者。主持国家自然科学基金项目、教育部高等学校博士点新教师基金项目、中国博士后科学基金特别资助和面上项目等4项。参与国家自然科学基金项目重点项目、面上项目等纵向课题项目。在《Nonlinear Dynamics》、《Transportation Research Part C\E》、《Journal of Statistical Mechanics: Theory and Experiment》、《The European Physical Journal B》、《Chinese Physics B》等刊物上发表学术论文30余篇。申请专利近60项，其中一作授权专利35项，获批软件著作权9项。
查看全部
指导本科生创新创业训练项目10项，其中，国家级4项，省级2项，校级4项。指导本科毕设获校级优秀毕设6次。指导本科生获得2023年The Interdisciplinary Contest in Modeling（ICM）大赛Finalist（特等奖提名，前3%）奖项。指导本科生获得第五届安徽省交通科技大赛一等奖。指导学生获得第29届智能交通世界大会创新大赛第二届“姑苏杯”青年智能交通创新技术应用大赛高校专题赛二等奖，获得校级互联网+、交通科技等大学生大赛金奖、银奖等10余项。指导研究生获得中国研究生数学建模竞赛二等奖。主持2022年度安徽省新时代育人质量工程项目（省级研究生教育教学改革研究）1项。获安徽省教学成果奖二等奖1项（排序第6）。
-
凌翔
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
凌翔，副教授，硕士生导师
查看全部
合肥工业大学运输与物流工程系系主任，主要研究方向为复杂网络、网络交通动力学、网络集群动力学、网络同步动力学。近年来，先后主持过多项国家级、校级科研基金，包括国家自然科学青年基金、国家自然科学主任基金、教育部博士点新教师基金、学术新人提升计划B类、重点实验室自主创新专项等等。在国内外重要期刊上发表论文20余篇，包括在领域著名期刊《Physical Review E》、《Chaos》、《Europhysics Letters》、《European Physical Journal B》、《Journal of Statistical Mechanics》、《Physics Letter A》、《Physica A》、《Chin. Phys. B》等，2018年获教育部自然科学一等奖1项。现任学术期刊《Journal of Statistical Mechanics》、《Physics Letter A》、《Physica A》、《Chin. Phys. B》审稿人，安徽省非线性科学学会理事等。
近年来，团队聚焦复杂网络科学，在网络信息流、网络交通等方面开展研究，欢迎交通、信息和计算机专业背景的同学和老师加入团队！
-
刘昊翔
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
目前主要从事交通运输管理领域的基础理论研究与应用，在城市交通网络设计建模、交通行为分析、交通规划管理与控制、电动汽车充换电设备选址、公共交通运营优化、数学优化算法等方面具有多年持续深入的研究与实践经验。先后发表期刊会议论文二十余篇，其中两篇入选ESI高被引论文。近年在城市交通网络设计领域等开展了持续而深入的研究工作，取得了一系列的研究成果，研究论文发表或录用在交通科学与技术领域顶级期刊《Transportation Research Part B》和国际知名期刊《Transportation Research Part E》、《Networks and Spatial Economics》及《Transportmetrica A》等上。
查看全部
-
于旸
合肥工业大学 ｜ 汽车与交通工程学院
研究方向：
查看全部
动态交通分配，交通系统建模、仿真、优化，复杂交通网络，交通规划，交通行为，交通大数据
发表论文：
Yu,Y., Han,K., Ochieng,W.O., 2020. Day-to-Day Dynamic Traffic Assignment with Imperfect Information, Bounded Rationality and Information Sharing.
Transportation Research Part C 114 (2020), 59-83.Yang Yu, Ke Han. Day-to-Day Dynamic Traffic Assignment with Imperfect Information and Information Sharing Behaviour. Transportation Research Board 99th Annual Meeting, Washington, D.C., Jan 2020.
教育经历：
西南交通大学 交通工程 2010.09 – 2014.06 学士
帝国理工学院 Transport 2014.10 – 2015.10 硕士
帝国理工学院 Transport 2016.06 – 2021.06 博士 .
-
龙建成
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 教授
龙建成，合肥工业大学教授、博士生导师。主要研究方向为城市交通网络优化与管理、城市动态交通分配理论与方法、共享交通系统建模与优化、公共交通运营与管理等。近年来，先后主持国家自然科学基金项目5项（包括青年基金、面上、优青、杰青）、教育部新世纪优秀人才支持项目、霍英东教育基金会高等学校青年教师基金项目、中国博士后科学基金项目、安徽省重大科技专项项目等；在国内外重要期刊上发表论文70余篇，包括在领域顶级期刊《Operations Research》上发表论文3篇（一作2篇）、《Transportation Science》上发表论文1篇（一作）、《Transportation Research Part B》上发表论文13篇（一作或通讯10篇）。其它论文主要发表在《Transportation Research Part C\D\E》、《IEEE Transactions on Intelligent Transportation Systems》、《European Journal of Operational Research》、《Networks and Spatial Economics》、《系统工程理论与实践》等期刊上。博士学位论文“城市道路交通拥堵传播规律及消散控制策略研究”获2012年全国优秀博士学位论文提名论文，2013年入选教育部新世纪优秀人才支持计划，动态交通分配方面的研究成果曾入选了国家自然科学基金委2014年年度报告，2015年获得国家自然科学基金优秀青年科学基金，2017年入选教育部“长江学者奖励计划”青年学者，2018年获教育部自然科学一等奖1项，1篇论文入选《中国科学》“2018年十年持续影响力论文奖”，2019年获得国家杰出青年科学基金，2021年获安徽省教科文卫体系统职业道德先进个人,2022年获安徽省教学成果二等奖1项。现任学术期刊《Digital Transportation and Safety》高级副主编、《控制与决策》和《交通运输系统工程与信息》等编委、管理科学与工程学会常务理事、安徽省非线性科学学会副理事长、管理科学与工程学会交通运输管理分会副主任等。
查看全部
-
丁建勋
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
合肥工业大学本科毕业（双专业：主修管理，辅修计算机）和博士后（管理科学与工程）出站，北京航空航天大学硕士和博士（交通运输规划与管理），东京大学西城教授课题组交流学者。主持国家自然科学基金项目、教育部高等学校博士点新教师基金项目、中国博士后科学基金特别资助和面上项目等4项。参与国家自然科学基金项目重点项目、面上项目等纵向课题项目。在《Nonlinear Dynamics》、《Transportation Research Part C\E》、《Journal of Statistical Mechanics: Theory and Experiment》、《The European Physical Journal B》、《Chinese Physics B》等刊物上发表学术论文30余篇。申请专利近60项，其中一作授权专利35项，获批软件著作权9项。
查看全部
指导本科生创新创业训练项目10项，其中，国家级4项，省级2项，校级4项。指导本科毕设获校级优秀毕设6次。指导本科生获得2023年The Interdisciplinary Contest in Modeling（ICM）大赛Finalist（特等奖提名，前3%）奖项。指导本科生获得第五届安徽省交通科技大赛一等奖。指导学生获得第29届智能交通世界大会创新大赛第二届“姑苏杯”青年智能交通创新技术应用大赛高校专题赛二等奖，获得校级互联网+、交通科技等大学生大赛金奖、银奖等10余项。指导研究生获得中国研究生数学建模竞赛二等奖。主持2022年度安徽省新时代育人质量工程项目（省级研究生教育教学改革研究）1项。获安徽省教学成果奖二等奖1项（排序第6）。
-
凌翔
合肥工业大学 ｜ 汽车与交通工程学院 ｜ 副教授
凌翔，副教授，硕士生导师
查看全部
合肥工业大学运输与物流工程系系主任，主要研究方向为复杂网络、网络交通动力学、网络集群动力学、网络同步动力学。近年来，先后主持过多项国家级、校级科研基金，包括国家自然科学青年基金、国家自然科学主任基金、教育部博士点新教师基金、学术新人提升计划B类、重点实验室自主创新专项等等。在国内外重要期刊上发表论文20余篇，包括在领域著名期刊《Physical Review E》、《Chaos》、《Europhysics Letters》、《European Physical Journal B》、《Journal of Statistical Mechanics》、《Physics Letter A》、《Physica A》、《Chin. Phys. B》等，2018年获教育部自然科学一等奖1项。现任学术期刊《Journal of Statistical Mechanics》、《Physics Letter A》、《Physica A》、《Chin. Phys. B》审稿人，安徽省非线性科学学会理事等。
近年来，团队聚焦复杂网络科学，在网络信息流、网络交通等方面开展研究，欢迎交通、信息和计算机专业背景的同学和老师加入团队！
龙建成
Course section课程章节
-
第1章 第一章 运筹学概论
-
1.1
运筹学的简史
[2024-01-25]
查看 -
1.2
运筹学的性质和特点
[2024-01-25]
查看 -
1.3
运筹学的工作模型
[2024-01-25]
查看 -
1.4
运筹学的模型
[2024-01-25]
查看 -
1.5
运筹学的应用
[2024-01-25]
查看 -
1.6
运筹学的展望
[2024-01-25]
查看
-
1.1
运筹学的简史
-
第2章 线性规划与单纯形法
-
2.1
线性规划问题及其数学模型
[2024-01-25]
查看 -
2.2
线性规划问题的几何意义
[2024-01-25]
查看 -
2.3
单纯形法
[2024-01-25]
查看 -
2.4
单纯性法的计算步骤
[2024-01-25]
查看 -
2.5
单纯形法的进一步讨论
[2024-01-25]
查看 -
2.6
应用举例
[2024-01-25]
查看
-
2.1
线性规划问题及其数学模型
-
第3章 对偶理论和灵敏度分析
-
3.1
单纯形法的矩阵描述
[2024-01-25]
查看 -
3.2
单纯形法的矩阵计算
[2024-01-25]
查看 -
3.3
对偶问题的提出
[2024-01-25]
查看 -
3.4
线性规划的对偶理论
[2024-01-25]
查看 -
3.5
影子价格
[2024-01-25]
查看 -
3.6
对偶单纯形法
[2024-01-25]
查看 -
3.7
灵敏度分析
[2024-01-25]
查看 -
3.8
参数线性规划
[2024-01-25]
查看
-
3.1
单纯形法的矩阵描述
-
第4章 运输问题
-
4.1
运输问题的数学模型
[2024-01-25]
查看 -
4.2
表上作业法
[2024-01-25]
查看 -
4.3
产销不平衡的运输问题及其求解方法
[2024-01-25]
查看 -
4.4
应用举例
[2024-01-25]
查看
-
4.1
运输问题的数学模型
-
第5章 线性目标规划
-
5.1
目标规划的数学模型
[2024-01-25]
查看 -
5.2
解目标规划的图解法
[2024-01-25]
查看 -
5.3
解目标规划的单纯形法
[2024-01-25]
查看 -
5.4
应用举例
[2024-01-25]
查看
-
5.1
目标规划的数学模型
-
第6章 整数线性规划
-
6.1
整数线性规划问题的提出
[2024-01-25]
查看 -
6.2
分支定界法
[2024-01-25]
查看 -
6.3
割平面法
[2024-01-25]
查看 -
6.4
0-1型整数线性规划
[2024-01-25]
查看 -
6.5
指派问题
[2024-01-25]
查看
-
6.1
整数线性规划问题的提出
-
第7章 无约束问题
-
7.1
基本概念
[2024-01-25]
查看 -
7.2
一维搜索
[2024-01-25]
查看 -
7.3
无约束极值问题的解法
[2024-01-25]
查看
-
7.1
基本概念
-
第8章 约束极值问题
-
第9章 动态规划的基本方法
-
9.1
多阶段决策过程及实例
[2024-01-25]
查看 -
9.2
多阶段决策过程及实例
[2024-01-25]
查看 -
9.3
动态规划的基本概念和基本方程
[2024-01-25]
查看 -
9.4
动态规划的最优性原理和最优性定理
[2024-01-25]
查看 -
9.5
动态规划和静态规划的关系
[2024-01-25]
查看
-
9.1
多阶段决策过程及实例
-
第10章 动态规划应用举例
-
10.1
资源分配问题
[2024-01-25]
查看 -
10.2
背包问题
[2024-01-25]
查看 -
10.3
生产与存储问题
[2024-01-25]
查看 -
10.4
货郎担问题
[2024-01-25]
查看
-
10.1
资源分配问题
-
第11章 图与网络优化
-
11.1
图的基本概念
[2024-01-25]
查看 -
11.2
树
[2024-01-25]
查看 -
11.3
最短路问题
[2024-01-25]
查看 -
11.4
网络最大流问题
[2024-01-25]
查看 -
11.5
最小费用最大流问题
[2024-01-25]
查看 -
11.6
中国邮递员问题
[2024-01-25]
查看
-
11.1
图的基本概念
展开更多
Curriculum evaluation课程评分
“教学重难点突出，授课步骤设计合理，由浅入深，循序渐进。”
2024-01-26 15:38
“内容非常充实，涵盖了广泛的知识点， 老师讲解的清晰易懂，更好的激发了学习兴趣。收获满满！ ”
2024-01-26 15:15
“课程设计非常有深度和广度，逻辑清晰，思想明确，受益良多 ”
2024-01-26 15:13
“课程讲的很细致通俗易懂，还配有案例讲解，解题原理和步骤讲的很清楚很详细，学到了很多知识”
2024-01-26 15:11
“课程知识量充实，趣味性丰富，设计合理，形式丰富！通过运筹学的学习能够在很大程度上系统化、模型化实际生产生活中的问题并进行快速、有效的解决，受益匪浅！”
2024-01-26 15:05
“老师们讲的非常细致，知识连贯，课程内容丰富，学到了许多知识。 ”
2024-01-26 15:03
“内容详略得当，讲解深入浅出，希望以后能把 运筹学的原理方法用在实践中！”
2024-01-26 14:57
“不仅帮我学会了运筹学来解决问题，还深入理解了基本原理。”
2024-01-26 14:26
参考教材
运筹学第4版（清华大学出版社）
课程安排
| 周次 | 讲次 | 学时（分钟） | 教学内容（要点） |
| 1 | 1 | 2（100） | 运筹学的简史、性质、特点及应用 |
| 1 | 2 | 2（100） | 线性规划问题模型及几何意义 |
| 2 | 3 | 2（100） | 单纯形法原理、单纯形法的计算步骤 |
| 2 | 4 | 2（100） | 单纯形法的进一步讨论、应用举例 |
| 3 | 5 | 2（100） | 线性规划的对偶理论 |
| 3 | 6 | 2（100） | 线性规划的灵敏度分析 |
| 4 | 7 | 2（100） | 运输问题的数学模型、表上作业法 |
| 4 | 8 | 2（100） | 产销平衡运输问题的求解方法，产销不平衡运输问题的求解方法，应用举例 |
| 5 | 9 | 2（100） | 图与网络中的基本概念 |
| 5 | 10 | 2（100） | 理解网络分析的基本方法 |
| 6 | 11 | 2（100） | 树，图的支撑树、最小支撑树问题 |
| 6 | 12 | 2（100） | 最短路径问题 |
| 7 | 13 | 2（100） | 网络最大流问题、最小费用最大流问题 |
| 7 | 14 | 2（100） | 分支定界法、割平面解法 |
| 8 | 15 | 2（100） | 0-1型整数规划、指派问题 |
| 8 | 16 | 2（100） | 无约束问题的基本概念；一维搜索法；无约束极值问题的解法 |
| 9 | 17 | 2（100） | 斐波那契搜索法、0.618搜索法 |
| 9 | 18 | 2（100） | 非线性约束极值问题的基本概念 |
| 10 | 19 | 2（100） | 非线性约束问题最优性条件、库恩-塔克条件 |
| 10 | 20 | 2（100） | 二次规划；可行方向法；制约函数法 |
| 12 | 21 | 2（100） | 多阶段决策过程及实例；动态规划的基本概念和基本方程 |
| 12 | 22 | 2（100） | 动态规划的最优性原理和最优性定理；动态规划应用举例 |
| 13 | 23 | 2（100） | 排队论基本概念、排队系统分析 |
| 13 | 24 | 2（100） | 单服务台负指数分布排队系统的分析 |
课程视频
运筹学的由来
在公元前3世纪的楚汉相争中，汉高祖刘邦的著名谋士张良为推翻秦朝，打败项羽，统一全国立下了盖世奇功，刘邦赞誉他“夫运筹策帷帐之中，决胜于千里之外”。这千古名句也可以说是对张良的运筹思想的赞颂和褒奖，《史记》在《留侯世家》及其他多处也曾提及。这里的“运筹”，指张良在帷幄中制定作战谋略与决策的过程。在西汉时代，“运筹”已被当作制定谋略与决策职能分工的代名词。
我国1955年开始研究运筹学时，从《史记》中摘取“运筹”一词作为“ Operations Research”的意译，包含了运用筹划、以智取胜的深刻含义。从《史记》中对“运筹”的记述表明，我国的运筹学思想源远流长，至今对运筹学的发展仍有重要影响。
古今运筹故事
1、田忌赛马
孙膑的“斗马术”是我国古代运筹思想中争取总体最优的脍炙人口的著名范例。齐将田忌与齐王赛马，孙膑献策：以下马对齐王上马,以上马对齐王中马，以中马对齐王下马结果田忌以负两胜而获胜。
启示：①要善于用局部的牺牲去换取全局的胜利，从而达到以弱胜强的目的。它的基本思想是不强求一局的得失，而争取全盘的胜利。这是一个典型的博弈问题。
2、围魏救赵
公元前368年，赵国在齐国支持下，出兵攻打魏国的属国卫国。魏惠王派大将庞涓率兵近十万围攻赵国的国都邯郸。赵国只得向齐国求救。齐威王以田忌为大将、孙膑为军师，出兵八万救赵。身为军师的孙膑在分析形势后，认为魏国军队很强大，如果与魏军正面交锋会造成齐国的较大损失，所以应该避实就虚，趁着魏国精锐部队在外，魏国国都大梁防务空虚的机会，攻打它的国都，迫使魏军回救大梁，赵国的危险就会自然消解。为争取战略主动，孙膑决定给敌军制造齐国部队弱小的假象。他故意派无能的军官带兵进攻魏国的军事重镇平陵，结果齐军大败。魏国大将庞涓以为齐军不堪一击，于是加紧对赵国的进攻，丝毫没有想到齐军会攻打魏国的国都大梁。与此同时，孙膑亲自率领精锐部队进逼魏国国都大梁。庞涓闻讯，迅猛从攻打赵国的前线往回撤军，长途跋涉去保卫国都。因为兵困马乏，又陷入孙膑的包围圈中，结果魏军被打得落花流水。
启示：①充分体现了如何筹划兵力，选择最佳时间、地点，趋利避害，集中优势兵力以弱克强的运筹学思想②为了达到某个预定目的，如果直接去做，可能会得不偿失，甚至适得其反。但如果从另一个角度去做，可能就会取得事半功倍的效果。
3、丁谓建宫
宋真宗大中祥符年间(公元1008一1017年),都城开封里的皇宫失火，需要重建。右谏议大夫、权三司使丁渭受命负责限期重新营造皇宫建造皇宫需要很多土,丁渭考虑到从营建工地到城外取土的地方距离太远，费工费力。丁渭便下令将城中街道挖开取土，节省了不少工时。挖了不久，街道便成了大沟。丁渭又命人挖开官堤，引汴河水进入大沟之中，然后调来各地的竹筏木船经这条大沟运送建造皇宫所用的各种物材，十分便利。等到皇宫营建完毕，渭命人将大沟中的水排尽，再将拆掉废旧皇宫以及营建新皇宫所丢弃的砖头瓦砾添入大沟中，大沟又变成了平地，重新成为街道。这样，丁渭一举三得，挖土、运送物材、处理废弃瓦砾等三项工程一蹴而成，节省的工费数以亿万计。
启示：这是我国古代大规模工程施工组织方面运筹思想的典型例子。
“交通+运筹”
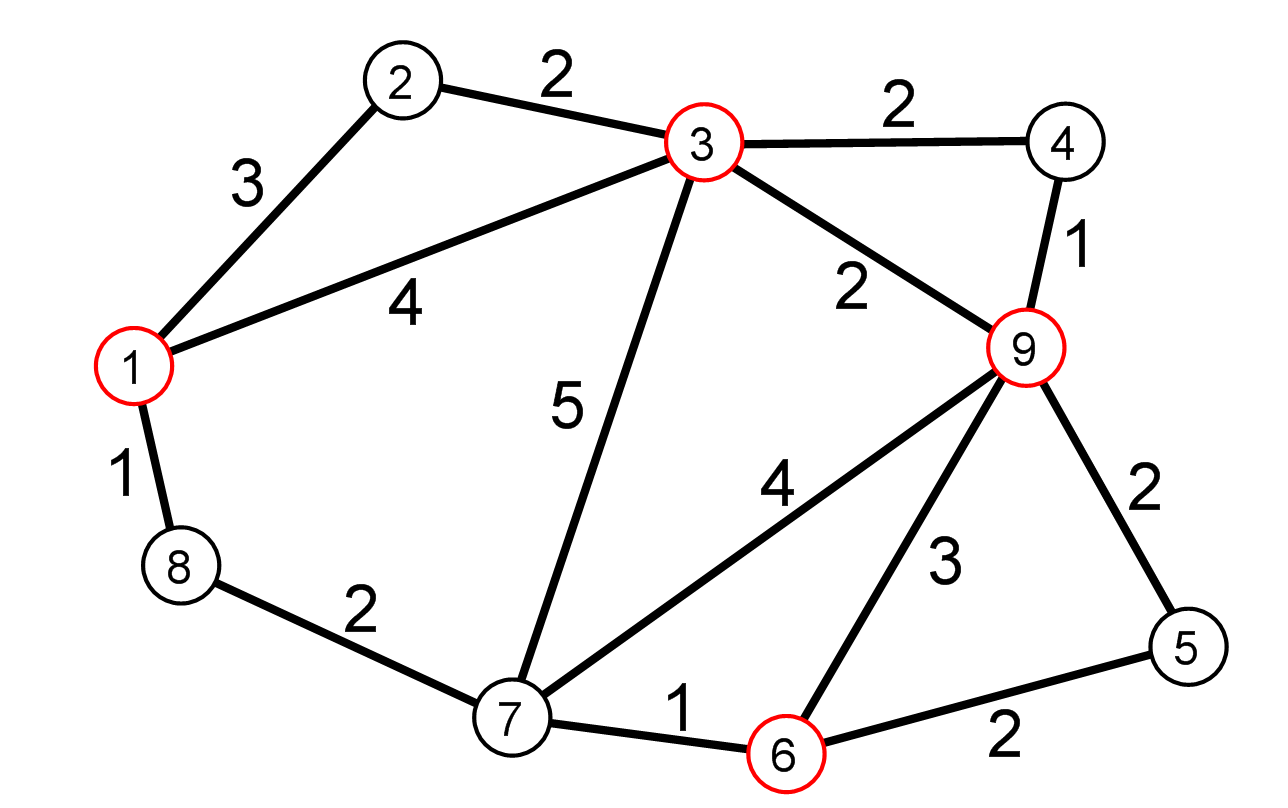
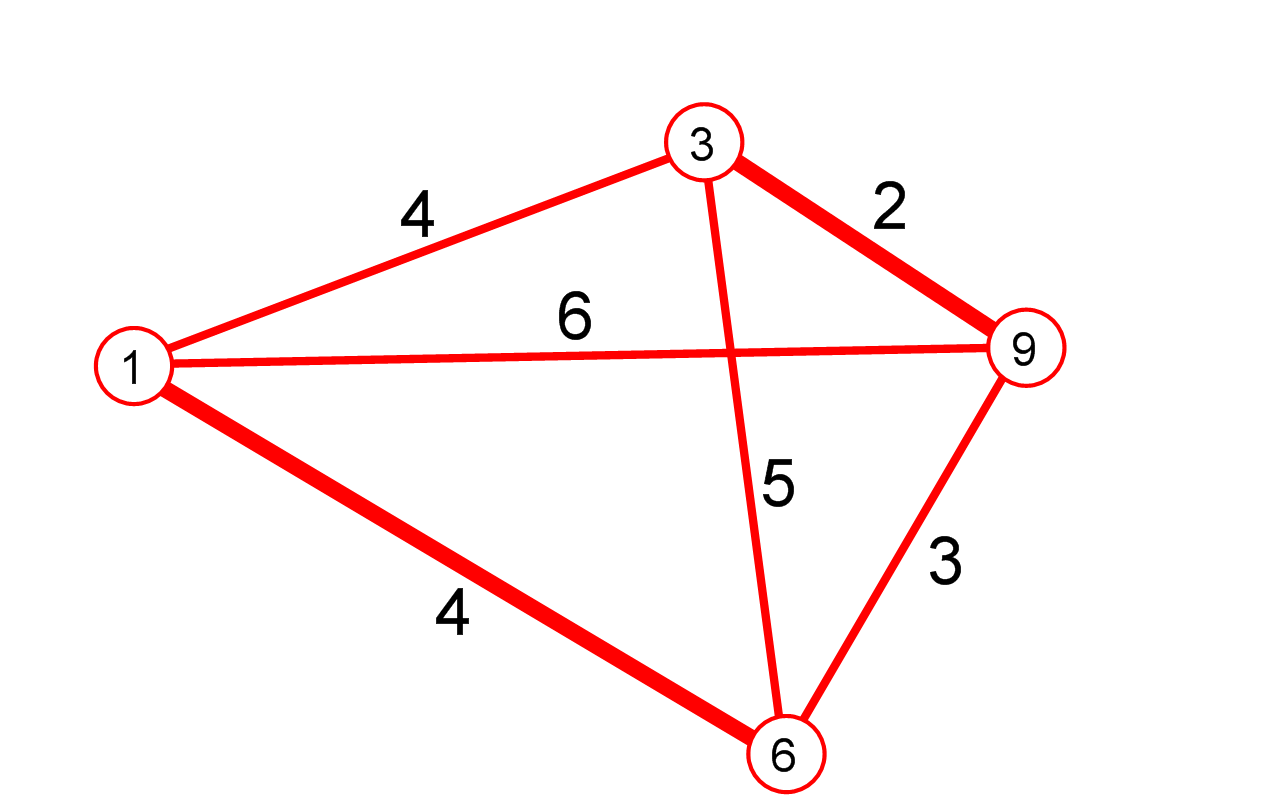
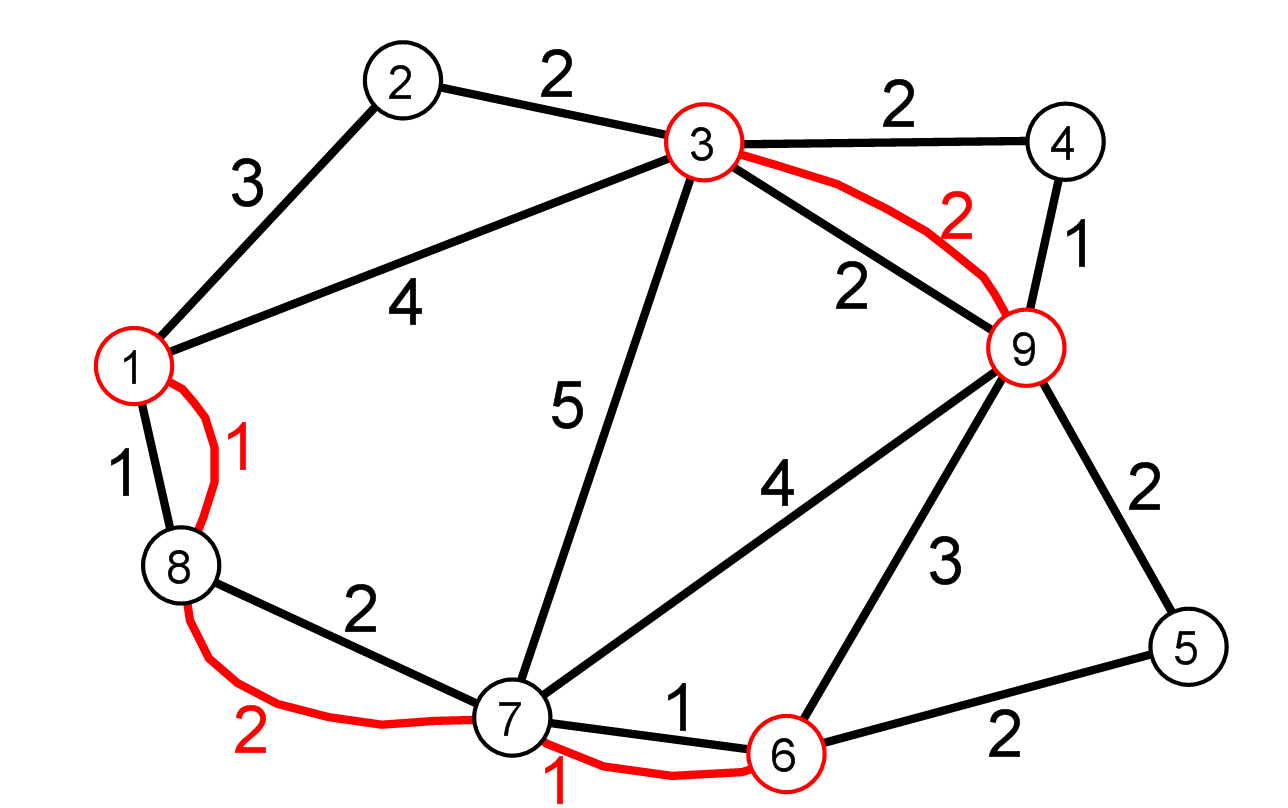
1、最短路问题
用Dijkstra方法求从到个点的最短路
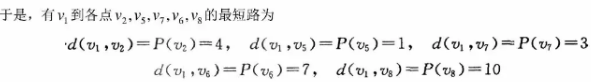
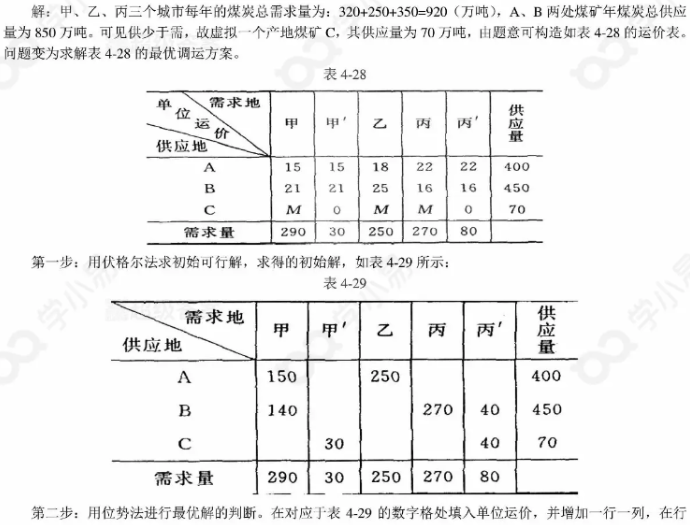
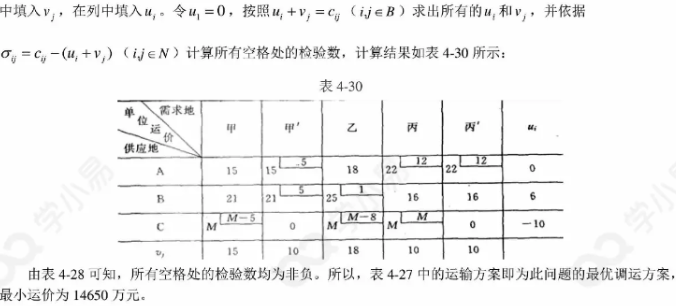
2、运输问题
甲、乙、丙三个城市每年需要煤炭分别为：320万吨、250万吨、350万吨，由A、B两处煤矿负责供应。已知煤炭年供应量分别为：A——400万吨，B——450万吨。煤矿至各城市的单位运价(万元/万吨)见表2-1。由于需大于供，经研究平衡决定，甲市供应量可减少0～30万吨，乙城市需要量应全部满足，丙城市供应量不少于270万吨。试求将供应量分配完又使总运费为最低的调运方案。
表2-1
| 甲 | 乙 | 丙 | |
| A | 15 | 18 | 22 |
| B | 21 | 25 | 16 |
3、旅行商（TSP)）问题
求解六个城市旅行推销员问题。其距离矩阵如表3-1所示所示。设推销员从1城出发，经过每个城市一次且仅一次，最后回到1城。问按怎样的路线走，使总的程最短。
表3-1
j | i | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 10 | 20 | 30 | 40 | 50 |
| 2 | 12 | 0 | 18 | 30 | 25 | 21 |
| 3 | 23 | 9 | 0 | 5 | 10 | 15 |
| 4 | 34 | 32 | 4 | 0 | 8 | 16 |
| 5 | 45 | 27 | 11 | 10 | 0 | 18 |
| 6 | 56 | 22 | 16 | 20 | 12 | 0 |
4、轮船调度问题
某航运公司承担六个港口城市A、B、C、D、E、F的四条固定航线的物资运输任务。已知各条航线的起点、终点城市及每天航班数见表4-1。假定各条航线使用相同型号的船只，又各城市间的航程天数见下表4-2。又知道每条船每次装卸货的时间各需1天，则该航运公司至少应该配备多少条船，才能满足所有航线的运货需求？
表4-1
| 航线 | 起点城市 | 终点城市 | 每天航班数 |
| 1 | E | D | 3 |
| 2 | B | C | 2 |
| 3 | A | F | 1 |
| 4 | D | B | 1 |
表4-2
起点 | 终点 | |||||
| A | B | C | D | E | F | |
| A | 0 | 1 | 2 | 14 | 7 | 7 |
| B | 1 | 0 | 3 | 13 | 8 | 8 |
| C | 2 | 3 | 0 | 15 | 5 | 5 |
| D | 14 | 13 | 15 | 0 | 17 | 20 |
| E | 7 | 8 | 5 | 17 | 0 | 3 |
| F | 7 | 8 | 5 | 20 | 3 | 0 |
(1)载货航程需要的周转船只数量。例如航线1，在港口E装货1天，E到D航程17天，在D卸货1天，总计19天。每天3航班，故该航线周转船只需要57条。各条航线所需船只数量见下表4-3.以上累计共需周转船只数量为91条。
表4-3
| 航线 | 装货天数 | 航程天数 | 卸货天数 | 小计 | 航班数 | 需要周转船只数量 |
| 1 | 1 | 17 | 1 | 19 | 3 | 57 |
| 2 | 1 | 3 | 1 | 5 | 2 | 10 |
| 3 | 1 | 7 | 1 | 9 | 1 | 9 |
| 4 | 1 | 13 | 1 | 15 | 1 | 15 |
（2）各港口间调度所需船只数。有些港口每天到达船数多于需要船数，例如港口D，每天到达3条，需求1条；而有些港口到达数少于需求数，例如港口B。各港口每天余缺船只数的计算见表4-4。
表4-4
| 港口城市 | 每天到达 | 每天需求 | 余缺数量 |
| A | 0 | 1 | -1 |
| B | 1 | 2 | -1 |
| C | 2 | 0 | 2 |
| D | 3 | 1 | 2 |
| E | 0 | 3 | -3 |
| F | 1 | 0 | 1 |
为了使配备船只数量最少，应该做到周转的空船数量最少。因此建立以下运输问题，其产销平衡表如下表4-5.
表4-5
| 港口 | A | B | E | 每天多余船只 |
| C | 2 | |||
| D | 2 | |||
| F | 1 | |||
| 每天缺少船只 | 1 | 1 | 3 |
单位运价表应为相应各个港口之间的船只航程天数，见表4-6.
表4-6
| 港口 | A | B | E |
| C | 2 | 3 | 5 |
| D | 14 | 13 | 17 |
| F | 7 | 8 | 3 |
用表上作业法求出空穿的最优调度方案，见表4-7.
表4-7
| 港口 | A | B | E | 每天多余船只 |
| C | 1 | 1 | 2 | |
| D | 1 | 1 | 2 | |
| F | 1 | 1 | ||
| 每天缺少船只 | 1 | 1 | 3 |
由表4-7可知最少需要周转的空船只的数量为2×1+13×1+5×1+17×1++3×1=40（条）
在不考虑维修、储备等情况下，该公司至少应该配备40+91=131条船。
